Introduction

We're officially done with mechanics (well, that is assuming that you did everything in order). Now, we're diving into the wild world of electricity and magnetism. A fair word of warning here: this topic is much less intuitive than mechanics, because it's not possible to visualize many of the effects we talk about in this section. Nevertheless, this is a fundamental topic in physics and one that is very crucial to understand if you have a geunine interest in physics.

Definition

First, we'll start with defining the most fundamental part of electricity: electric charge. It is something that is very hard to visualize, much like mass. However, unlike mass, which we can "feel" through the weight of objects, there is no way for us to "feel" electric charge (unless you count getting electrocuted). Much like mass, it is a fundamental physical property of matter.

As a fundamental quantity, charge is always conserved. Like energy, we can say that charge can never be created or destroyed, in a law we call the conservation of electric charge. The first thing we need to know is that electricity and magnetism deals with something called electric charge. It's hard to pin a definition on what it is, but I assume that you've had some exposure to it before. It is fundamental, and can never be created or destroyed. Thus, we can write the law of conservation of electric charge.


This is an extremely simple definition, but it catches the essence of the concept pretty well. As you're probably aware, electric charge has a few nuances to it. You've probably heard of positive and negative charge. Well, those are the two kinds of electric charge, and the sign of the charge determines the behavior of the charged particles.

Mass only has one sign (as far as we're concerned): positive. Under gravitation, objects with mass interact through attraction; however, electric charge has slightly different behavior. Charges of the same sign will repel each other, and charges of opposite signs will attract. You have probably heard of this rule before, and it is referenced in the adage "opposite attract". This might seem like an extremely simple statement, but it is very helpful when you are analyzing other concepts. I'm going to say something that you've probably heard in your elementary school classes: Like charges repel, and opposite charges attract. It is really that simple. Keep this in mind, because it is very useful conceptually. It's not exactly the hardest thing in the world, but it does matter.

Insulators and Conductors

Before we talk about charge any further, we have to talk very briefly about material science. There are two main kinds of materials that we talk about in electricity and magnetism: conductors and insulators. They are classified based on how easily charge can move around within them.

A conductor is a material that allows the charges within it (these are the electrons of the material) to move around completely freely. These materials are usually used in wires in order to transfer electric current, but that's a discussion topic for later. The key characteristic that you need to know for now is that conductors allow charge to move and distribute freely. We will talk more about what this means later.

An insulator is a material that holds on to its electrons more tightly. The electrons can still move around to some extent, but they are heavily restricted in their movement when compared to conductors. The main thing to know for now is that insulators do not let charge move around freely within them.

Here's a very short table listing typical conductors and insulators. This is by no means comprehensive, but should give you a good idea of what is a conductor and what is an insulator. As a general rule of thumb, if a problem mentions metals, you can assume that it is talking about conductors, and if it mentions things like rubber, you can assume that it is talking about an insulator.

Conductor	Insulator
Copper	Rubber
Aluminum	Glass
Gold	Oil
Salt Water	Paper
Graphite	Diamond

Charging

If you remember from chemistry, all objects theoretically have equal numbers of protons and electrons, so they have zero net charge. Net charge is simply the sum of all the charges on an object. Charging is the process of giving objects a net electric charge. There are two primary methods of charging: by conduction or by induction.

Charging by conduction is exactly what it sounds like: charging objects by contact. This is the more familiar of the two types of charging, and the more intuitive one. There are actually two sub-categories to this, involving conductors and insulators. Charging a conductor is simple: you just bring another charged object in contact with it, and some of the charge is transferred to the conductor.

Charging an insulator is slightly more complex. You can rub two insulating materials, like rubber and fabric, against each other to separate charges by friction. In the case of a rubber rod rubbed onto a piece of fabric, the rubber gains a negative net charge and the fabric loses electrons to gain a positive net charge. This works with electically neutral conductors as well, so you can rub a steel rod on fabric for a similar effect. The exact hierarchy for what material will gain electrons depends on something called the triboelectric series , a list of materials from most negative (likely to gain electrons) to most positive (likely to give electrons).

Triboelectric Series

Material (Positive to negative)
Glass
Wool
Silk
Paper
Cotton
Rubber
Teflon

This is by no means a comprehensive table, and it isn't mentioned very much. However, it's pretty interesting and relevant, so I decided to include it. Charging by conduction just involves direct contact. It should be the simpler of the two kinds, though it still depends on the kind of material in use. Normally, if we have just a conductor, we can touch a charged object to it and some of the charge will transfer over. However, we can actually use friction to separate charges from two object, giving both of them a net charge. For instance, if we rub a rubber rob on a piece of fabric, the rod will gain a net negative charge and the fabric a net positive charge. There is more nuance to this, but this is enough information for a conceptual level.

The next concept of charging by induction is much more complex, so we will talk about it on the next page.

Charging by Induction

Charging by induction is a kind of charging that doesn't involve direct contact. That sounds odd and unintuitive, but I promise you when I explain it will make a lot more sense. However, in order to explain this concept, we need to explain the idea of an electrical ground.

The electrical ground is a hypothetical charge sink that can take in an infinte amount of charge and essentially distribute it such that it has no effect. In practice, nothing can take an infinite amount of charge, but we consider the Earth to be so large that it is can take in any amount of charge we redirect into it. (Hence the name.) An electrical ground is basically a place that can soak up a lot of charge. In practice, we consider the Earth as our ground, hence the name.

The process of charging by induction involves several steps. First, we take a neutral conducting object and a charged rod. We want to bring the charged rod close to the conducting object, which has the effect of causing the charges to separate. For simplicity, let's just say that the rod has a positive charge. Since the charges on the conductor can move freely, we will see electrons tend to flow to the side closer to the positive charge because of electrostatic attraction. This leads to half of the object being negative, and the other half being positive. We call this polarization, but the net charge is still zero.

Our next step is to connect the conductor to the ground while keeping the rod close. This allows more electrons to come up from the ground, which basically eliminates the net positive charge of the side of the object that was further from the rod. We then disconnect the ground and take the rod away, leaving a net negative charge on the conductor. We've just charged an object without contacting it! That's the essence of charging by induction.

Here's a diagram that basically summarizes what I was saying:

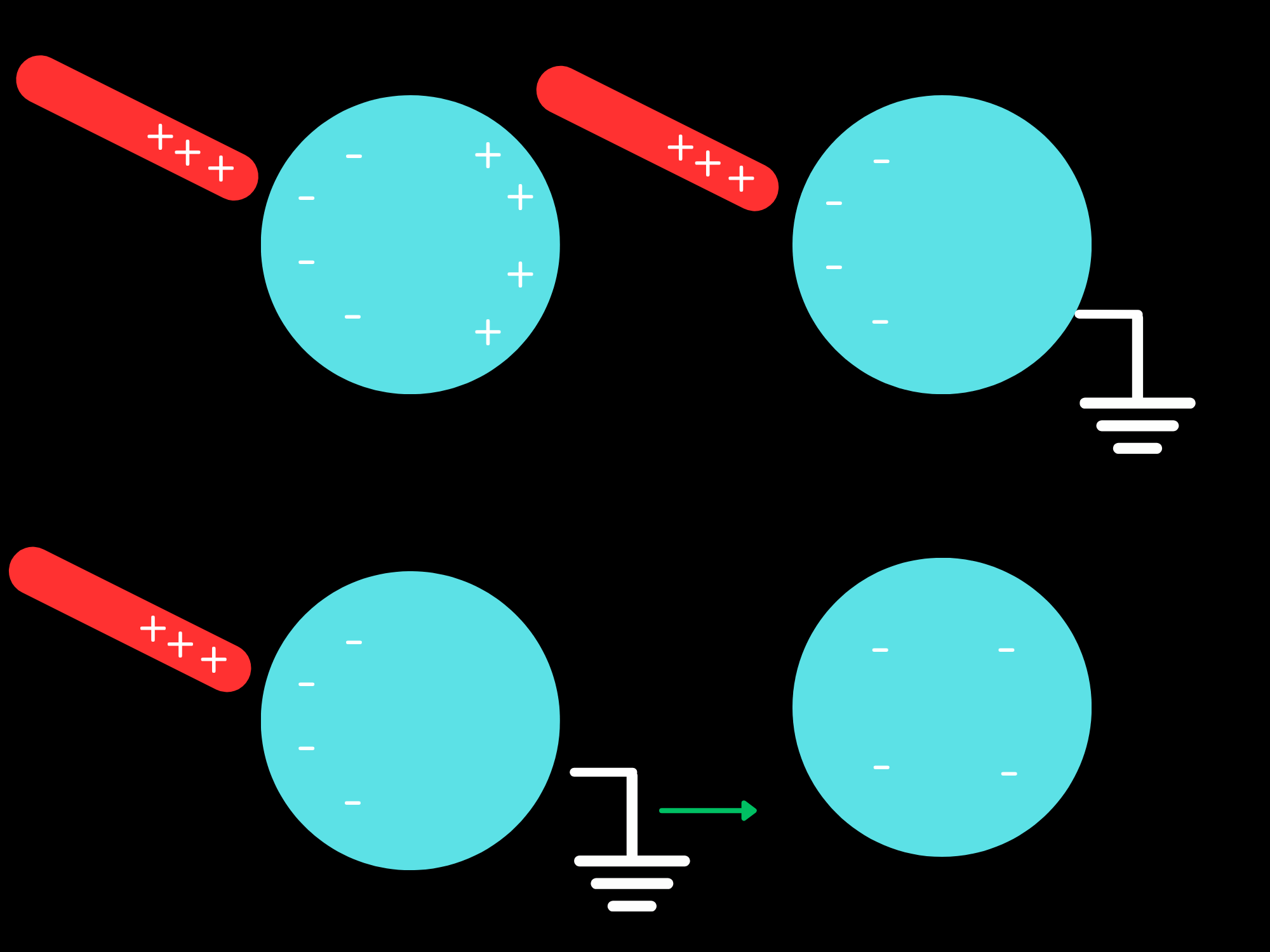
We need to keep in mind that charging by induction only works with conductors. Since insulators don't let charge flow freely, the charges can't separate in the first place, making this process impossible. Additionally, note that the final charge on the object is opposite to the charge of the rod. If we had a negative rod, the object would end up with a net positive charge. Just visualize the process again in your head and it should make sense.

With that, let's consider a problem that involves the idea of charging by conduction. I hope you've been paying attention, because this is a bit more complex than the basic example I gave earlier but works on the same principle.

The Fundamental Charge

Charge is actually not infinitely divisible. There is a fundamental charge that every other charge has to be a multiple of. This happens to be equal to the charge of an electron or proton, and we call it $e$. Note that the proton is positive, and the electron is negative.

$$ e = 1.602 \times 10^{-19}~\textrm{C} $$
The unit of charge there is called the coulomb, named after Charles-Augustin de Coulomb who studied electric forces. One coulomb of charge is a very large amount, so we usually deal with microcoulombs or nanocoulombs. On the topic of the fundamental charge again, every possible charge has to be an integer mutliple of this fundamental charge. That means not every amount of charge is possible!

With that, we can work on this concept with a very short practice problem.


Well, we just finished our very first lesson of electricity and magnetism! I know it might have seemed very simple, but I promise that the rest of this subject is not so easy. Do not let up on the simple things, because even though they might seem extremely easy they are foundational to understanding everything that comes after. With that, we're ready to talk about how charge attraction and repulsion works mathematically. If you're ready, just head on over to the next lesson!