Introduction

Play around with this one-dimensional collision demo for a bit to get a feel for what we're going to be dealing with!

Now, to explain what's going on. Essentially, you have two balls that collide with each other, with many parameters you can adjust. You might have noticed that changing some of the parameters can cause something different to happen. However, every collision here is unified by one thing: the fact that there are no net external forces on the system, ever. (Except when the balls bounce off the wall, but whatever.)

This means that we need to deal with this kind of situation as a momentum-conservation problem. The way we do that is by knowing that the total momentum of the system is zero. However, just knowing that isn't enough.

Types of Collisions

There are actually three types of collisions, classified on the basis of energy conservation. Recall that momentum will be conserved regardless of whether there are nonconservative internal interactions, but mechanical energy will not.

The first kind of collision is an elastic collision, where all mechanical energy is conserved. Usually, this just means that kinetic energy is conserved, since we're dealing with things that collide on a flat one-dimensional surface right now.

The next kind is an inelastic collision, where some mechanical energy is lost during the collision. This is a pretty general case that covers every case between the two extremes.

The final extreme is the totally inelastic collision, where the objects stick together and move as one after the collision. This is the case where the maximum possible amount of mechanical energy will be lost.

Not all of these are made equal. Problems wit totally inelastic collisions and elastic collisions get the majority of the spotlight because they are interesting both physically and mathematically, while inelastic collisions get sidelined a lot. I think this is for good reason, so I'll be perpetuating this trend.

Totally Inelastic Collisions

First, we'll work on the totally inelastic case.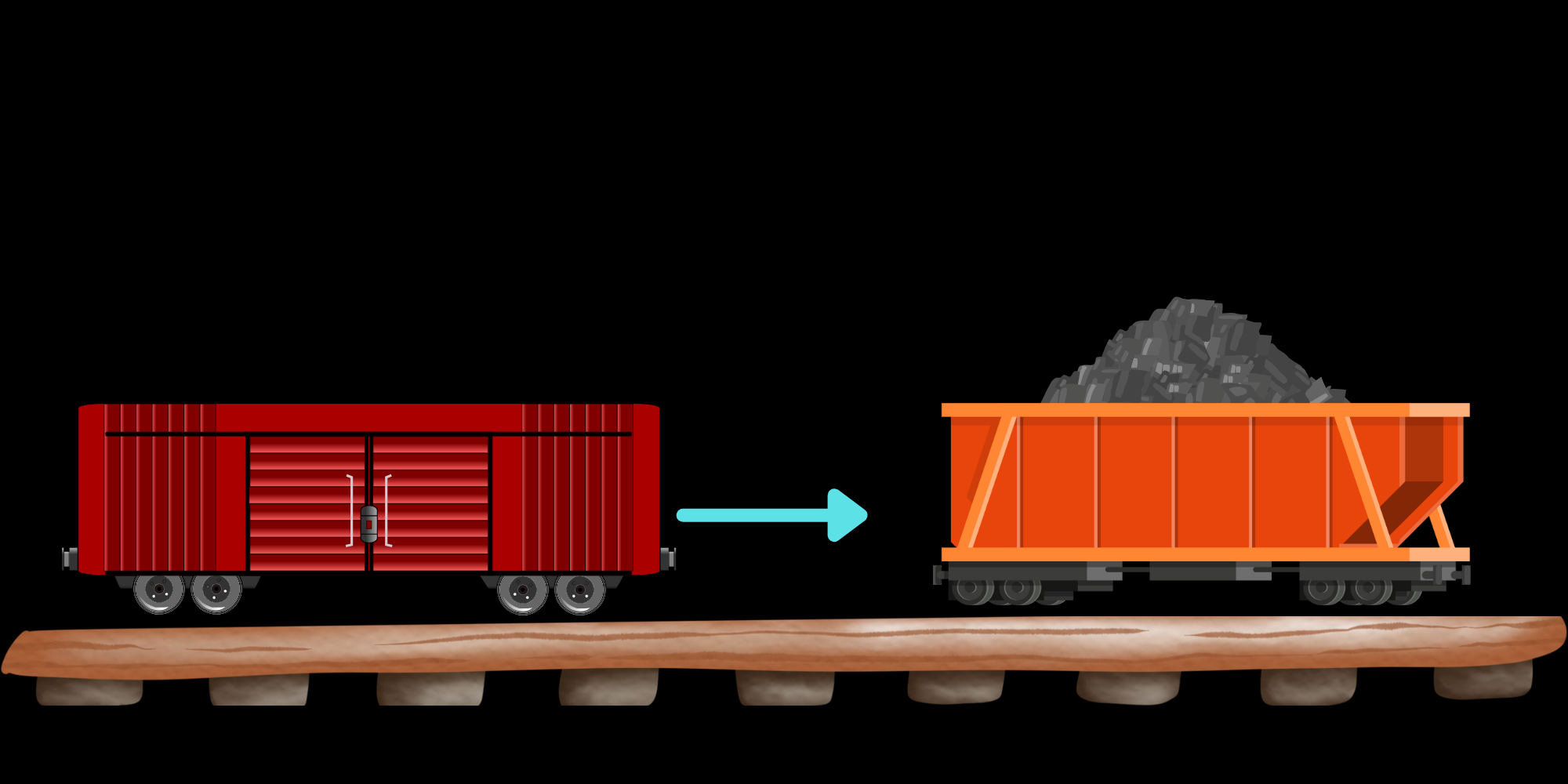

Two train cars are on a frictionless rail. The rear car is empty, having a mass of 700 kg. The forward car is loaded with coal and has a much larger mass of 5000 kg. Suddenly, the rear car is magically given a velocity of $v = 4.0 ~\textrm{m/s}$ towards the coal car. The cars couple together when they touch. What is their final velocity?

If you read carefully, it becomes obvious that this is a totally inelastic collision, since the two railway cars latch together after impact. This means they move with the same velocity, so we can essentially treat them as one object. With that knowledge, we can write momentum-conservation equations. This is done by setting total initial momentum equal to total final momentum.

$$ m_R v = (m_R + m_F) v_f $$
I have used the subscripts $R$ and $F$ to denote the rear and forward cars, respectively. This becomes a very easy problem to solve now. The algebraic manipulation and substitution should be simple, so I won't show it here.

$$ v_f = \bbox[3px, border: 0.5px solid white] { 0.491 ~\textrm{m/s} } $$

Elastic Collisions

The next case we're going to talk about is the elastic collision, where both mechanical energy and momentum are going to be conserved.

We can write the following two conditions for an elastic collision in this case:

$$ E = \textrm{const.} $$ $$ p = \textrm{const.} $$
For a system of two objects, this can be more concretely written. We'll assume we have all masses and write velocities in.

$$ \dfrac12 m_1 {v_{1i} }^2 + \dfrac12 m_2 {v_{2i} }^2 = \dfrac12 m_1 {v_{1f} }^2+ \dfrac12 m_2 {v_{2f} }^2$$
$$ m_1v_{1i} + m_2 v_{2i} = m_1 v_{1f} + m_2 v_{2f} $$
This does NOT look fun to deal with. If you're like me and are always looking for mathematical shortcuts to reduce your work, you're in luck here! You can derive a result that allows you to simplify your mathematical lives significantly. We just want to do a bit of algebraic mainpulation of the two equations above... (Disclaimer: I want to show the derivation, but I'm not expecting you to know it. Knowing the result is enough.)

$$ m_1 {v_{1i} }^2 - m_1 {v_{1f} }^2 = m_2 {v_{2f} }^2 - m_1 {v_{2i} }^2+ $$
$$ m_1v_{1i} - m_1 v_{1f} = m_2 v_{2f} - m_2 v_{2i} $$
Once we do some light algebra to both conservation equations, we can do a magical trick. I'm being sarcastic, it's just slightly tricky algebra. Remember the difference of squares? Are you seeing the vision? We can divide the two equations to arrive at the result:

$$ v_{1i} + v_{1f} = v_{2f} + v_{2i} $$
There's a better form to write this in that can be more helpful when solving problems.

$$ v_{1i} - v_{2i} = v_{2f} - v_{1f} $$
Let's unpack this equation. After moving the terms describing initial velocities and final velocities to their respective sides, we can see that both sides of the equation are expressions of relative velocity! To be specific, the equation states that the relative velocity of approach is equal to the relative velocity of recession between two objects undergoing an elastic collision!

This equation is actually a consequence of the fact that the center-of-mass velocity is constant in these scenarios. We can work in the center-of-mass frame, in which the total momentum must be zero because in that frame $ v_{cm} = 0 $$, and center of mass velocity is directly related to momentum. This is a different technique for these problems and a valid one, though it's not one I tend to use or talk about often.

The formula talks about relative velocity, so the signs that you see there are not set in stone. Just keep in mind the idea of relative velocity, and you'll be all good to use this equation for all your elastic-collision needs. Here's an exericse to test exactly that.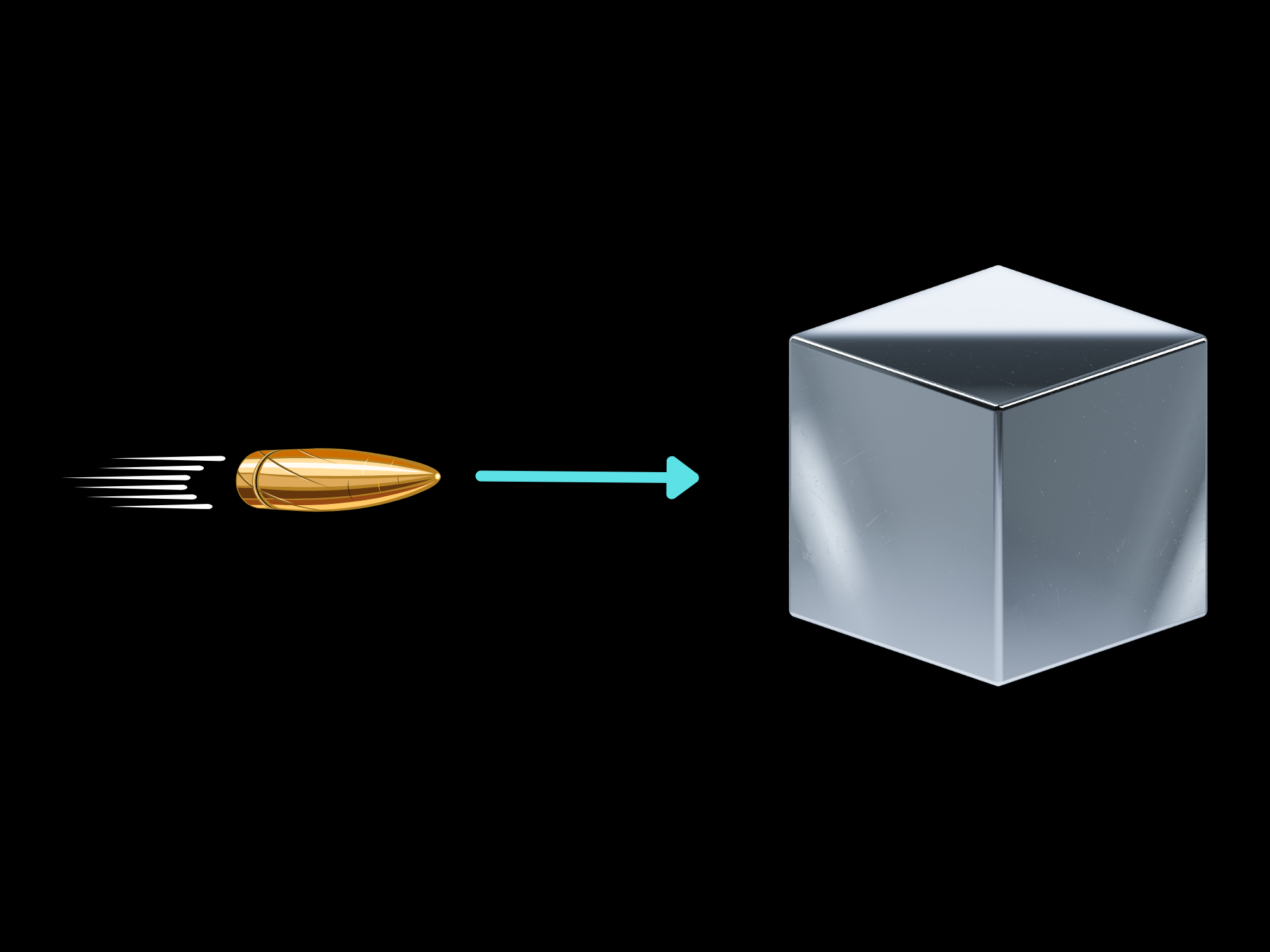

A tungsten bullet with a mass of 30 grams is fired at a metal cube that has a mass of 4.0 kg with a muzzle velocity of 1200 m/s. The bullet ricochets off the cube in a perfectly elastic one-dimensional collision. What are the final velocities of the bullet and cube?

This is just an elastic collision scenario. We know the initial masses and velocities of the objects, and we need to find their final velocities using our equations. First, we want to "guess" at the directions of motion of the objects after the collision. I'll say the bullet is going to the left, and the block will be going to the right. With this, we now have defined directions for our momentum vectors.

Here is our momentum conservation equation. I've defind bullet mass as $m$, block mass as $M$, and initial bullet velocity as $v_0$.

$$ mv_0 = M v_{Mf} - mv_{mf} $$
Now, we can write our second equation using the relative velocity relation.

$$ v_0 = v_{Mf} + v_{mf} $$
We add the velocities on the right side because both objects are receding from each other, meaning their relative velocity is the sum of their speeds. Now, we just need to do some simple algebra.

$$ mv_0 = M (v_0 - v_{mf}) - m v_{mf} $$
$$ (m+M) v_{mf} = (M-m) v_0 $$

This gives us the speed of the bullet after collision:

$$ v_{mf} = \bbox[3px, border: 0.5px solid white] {1182 ~\textrm{m/s} }$$
With this, we can find the speed of the block with a minimal amount of extra effort.

$$ v_{Mf} = v_0 - v{mf} = \bbox[3px, border: 0.5px solid white]{17.9 ~\textrm{m/s} }$$
That's the general gist of it!

I'm just going to wrap up any loose ends and special things I think should be mentioned in this unit. First off, for collisions sometimes you are given more information than is strictly necessary. In those cases (such as when you are given both initial velocities and one final velocity) do not overthink the problem, just do your momentum balance as always. I won't go over such problems because they are much simpler than what I've discussed previously.

Extreme Cases

We're going to mathematically derive all of the results here, so hang tight and be ready for some algebra! First, we'll see what happens when a small object of mass $m$ moving at some speed $v$ hits a very massive object of mass $M >> m$. This is basically like something hitting a brick wall.

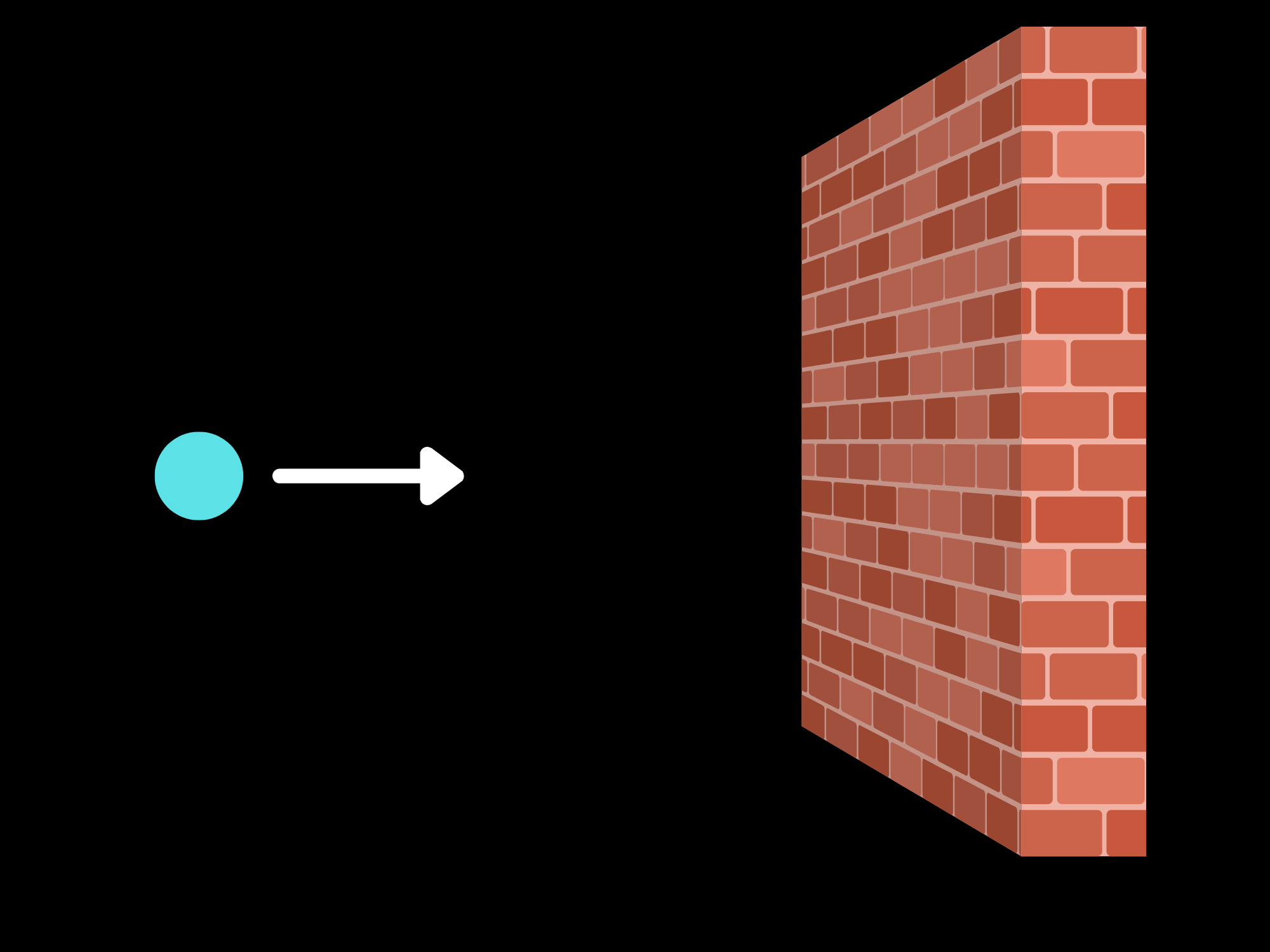
First, let's talk about the totally inelastic case. This is analogous to a blob of clay hitting the brick wall. Common sense tells us that it should just impact and stop, so let's see if the math tells us the same.

We can write our generic equations for the inelastic collison case:

$$ mv = (M+m) v_{f} $$
The special thing here is that $M >> m$. Keep this in mind. Now we solve for $v_f$:

$$ v_f = \dfrac{m}{M+m} v $$
This is the answer, but we can reduce it a little more. Since $ M >> m$, the denominator is much larger than the numerator. This means that we can approximate this as zero, since a very small number over a very large one is very close to zero!

$$ v_f \approx 0 $$
This is the expected result: when something hits and sticks to the brick wall, it stops moving. What about the elastic case?

In this case, we would expect the ball to rebound with the same speed, but in the opposite direction. Let's see if this is what we arrive at. We first still want to write our generic equations:

$$ mv = Mv_M - mv_m $$ $$ v = v_M + v_m $$
Now, we solve this just like we've done before.

$$ mv = M (v - v_m) - m v_m $$ $$ v_m = \dfrac{M-m}{M+m} v $$
Since $ M >> m$, we can see that the fraction should simplify to one. This is because the value of $m$ has a negligible effect on the actual value of the fraction, since $M$ is so much larger in this case. Therefore, we can write:

$$ v_m \approx v $$
This is what we expected! As a bonus, we can also see that the wall will have essentially no velocity after the collision, which is also the expected result. Physics wins again! (Wins over or against what, I have no idea. It just wins because it works. No mortal dares challenge the laws of physics.)

Now, I want to talk about a similar but likely less familiar case: the brick wall moving to hit the ball. Now, the ball is at rest initially, and the brick wall comes in and slams into it. The closest analogy I can think of for this is getting hit by an 18-wheeler truck.

First, let's do this mathematically. We're only going to consider the elastic case, because the inelastic case is quite easy to see: the object sticks to and moves with the "truck", moving at the same velocity the truck was initialyl going at. I'll leave the details of the reasoning for you to figure out, since we've done similar things in the past.

$$ Mv = mv_m + Mv_M$$ $$ v = v_m - v_M $$ $$ v_m = \frac{2M}{M+m} v $$
If we take the limiting case as we did before where $ M >> m$, we see that:

$$ v_m \approx 2v $$
Well, we can actually do some clever frame-of-reference tricks to arrive at the answer without having to do math. And, it explains why the answer is what it is in a much more natural way than numbers and equations. Let's work in the frame of reference moving with the mass $M$.

In this reference frame, we essentially have the case of the ball elastically bouncing off the brick wall. This means the final velocity of the ball in the frame moving with the large mass is $v_m' \approx v$.

We need to transform back into the original frame now, which means we move in the opposite direction of the mass $M$ at a speed of $v$. This means we need to add $v$ to the speed of $v_m'$ due to the transformation, letting us arrive at the aforementioned result:

$$ v_m \approx 2v$$

The interesting stuff happens when one object is much larger than another, sort of like a ball and a brick wall. That's not a perfect analogy, but it's good enough. First, we consider what happens if the smaller object is thrown at the wall.

There are two such cases: a totally inelastic collision with the wall, and a totally elastic one. Common sense should tell us what happens in each case, and I'll be relying more on intuition and general analysis rather than using momentum balance to prove the results. If you want to see the math, just head over to our algebra-based level.

In the totally inelastic case, we would expect the ball to stick to the wall and not move again. And that is indeed what momentum balance tells us would happen. The small and large objects stick together and move, but since the mass of the small object is so much less than that of the larger one, they would move so little we can just say they aren't moving.

What about the elastic case? Well, we should expect the ball to bounce off the wall with the same speed. This might not seem to conserve momentum because direction of motion is flipped, but remember that the wall would technically move forward with some very miniscule speed after the collision, which is enough to compensate for the disparity becaue mass is so large. Energy is also conserved for obvious reasons, since initial and final speeds are the same.

The most interesting case is when the large object moves and collides elastically with the small object. In this case, it's probably a better analogy to use an 18-wheeler truck as the large object. The elastic case is an interesting one, because we can see what happens just by using reference frame techniques.

If we transform into the frame where we move with the truck, which I'll say means we move to the left. Thus, we see the truck as stationary and the ball as moving to the right to hit it. Using the result from before, we know the ball will rebound with the same speed in the opposite direction. Now here comes the interesting part.

We transform back to the original reference frame, going from moving to the left with the truck to sitting "stationary". This means we effectively are moving to the right with some speed (the same speed as the truck), meaning we have to add that speed to the speed of the ball. Thus, the ball moves off with twice the velocity of the truck that approaches it after impact! Did you expect that?

Two-Dimensional Collisions

We know how to deal with collisions in one dimension, but what if we up that to two? (Or maybe even three?) It's actually not as bad as you would expect. Like many times before, we simply treat each dimension separately . Yes, this should remind you of force analysis and projectile motion.

There's not too much to say here. In general, for multiple dimensions, we can write the statements of momentum conservation for each dimension. It's important to remember that momentum is a vector quantity, and you can usually find the components by using trigonometry.

$$ p_x = \textrm{const.} $$ $$ p_y = \textrm{const.} $$ $$ p_z = \textrm{const.} $$
The only notable distinction that you should know is that the formula we gave for the relative velocities of approach and recession does not work for two-dimensional or three-dimensional collisions. The equation is a result of the center-of-mass velocity remaining constant, and in multiple dimensions the individual velocities typically do not lie in the same direction as the center-of-mass velocity.

With that, we can jump straight into a problem. For whatever reason, most of the time objects are represented with disks.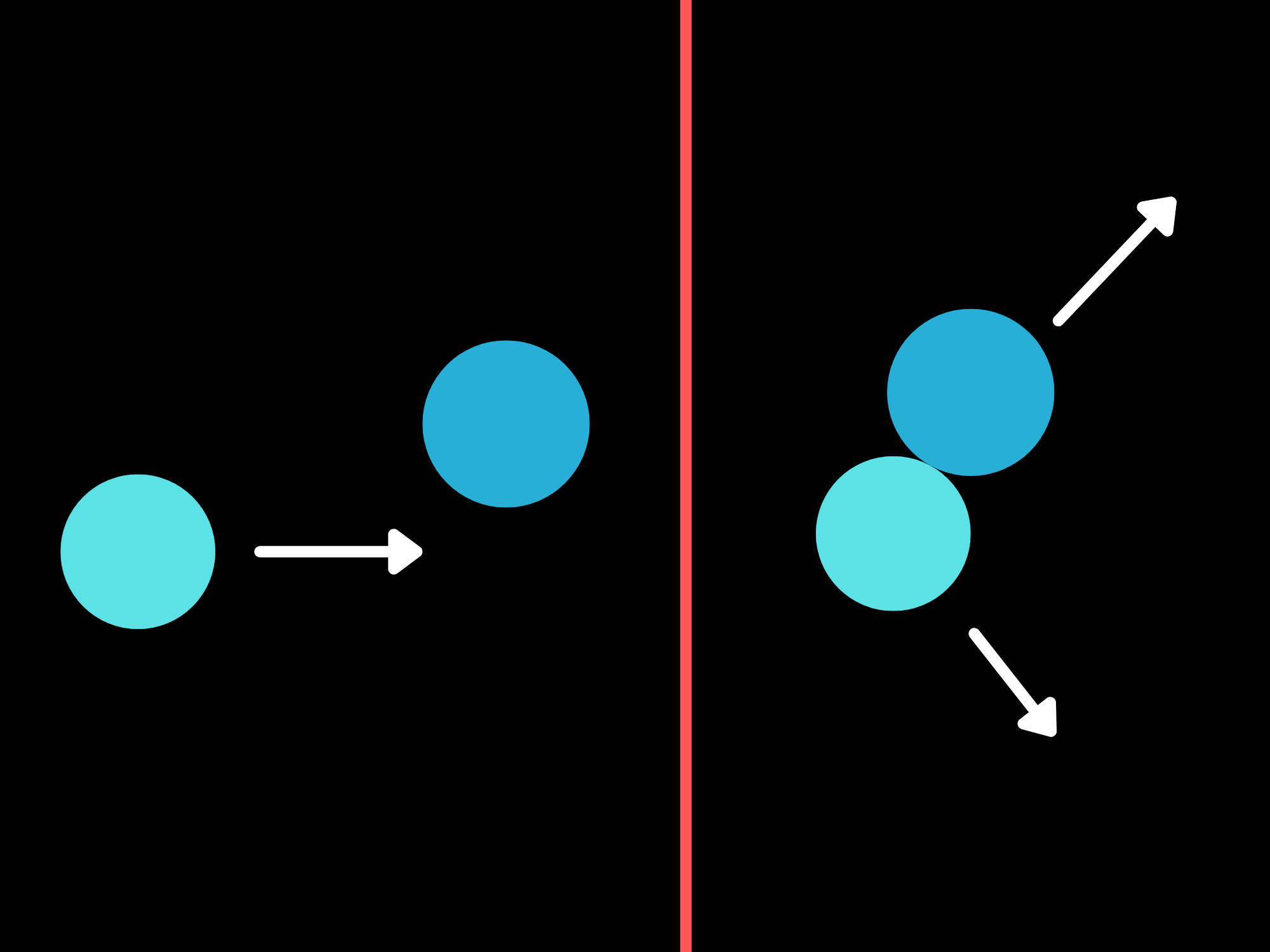

Two identical disks that hit each other elastically will always move off in directions that are pependicular to each other. Show this for the case of one disk moving off at 60° above the horizontal after the collision.

Okay. So what do we do here? Well, first off we should define some things that aren't defined in the initial problem. We want to recognize that it's essentially asking for a scenario where one disk moves in with some velocity $v$ to hit another identical one. Afterwards, one of them (we'll call this object 1) moves off at 60° above the horizontal. How does the other one (object 2) move?

Let's do some momentum balance. First, we'll deal with the x-direction, where initally we have a momentum of $mv$ from the first disk moving in. We'll use trig and the angle $\theta$ to represent the angle we don't yet know.

$$ mv = m v_1\cos 60° + m v_2\cos \theta $$
This alone is not enough, since we have too many unknowns. But, we can also write momentum balance for the y-direction. This direction has zero momentum initially.

$$ m v_1 \sin 60° = m v_2 sin \sin \theta $$
We have three unknowns ($v_1$, $v_2$, and $\theta$) but only two equations. We just need one more! Think for a moment for what the third equation we need to use is. Did you say energy conservation? Well, regardless, that's what we need to write!

$$ \dfrac 12 mv^2 = \dfrac12 m {v_1}^2 + \dfrac12 m {v_2}^2 $$
We can next divide out $m$ from each equation to arrive at our three equations.

$$ v = v_1\cos 60° + v_2\cos \theta $$ $$ v_1 \sin 60° = v_2 \sin \theta $$ $$ v^2 = {v_1}^2 + {v_2}^2 $$
Algebra time! You can tell I'm really excited by the way I'm repeatedly smashing my head into the wall. But in all seriousness, the only difficult part of multi-dimensional collisions is the math. The concepts are really similar, but the algebra...

First, we combine the first two equations, eliminating $v_2$. You can eliminate $v_1$ as well, it makes no difference. Oh, and we evaluate the trig to the exact expressions. Hope you remember your common angles!

$$ v = \dfrac12 v_1 + \dfrac{\sqrt{3} }{2} v_1 \dfrac{1}{\tan \theta} $$ $$ 2v = v_1 (1 + \dfrac{\sqrt{3} }{\tan \theta}) $$
We now eliminate $v_2$ from the third equation as well, using the same method.

$$ v^2 = {v_1}^2 + {v_1}^2 \frac{3}{4 \sin^2 \theta} $$ $$ v = v_1 \sqrt{1+ \dfrac{3}{4 \sin^2 \theta} } $$
Now, we divide both equations to elminate both $v$ and $v_1$ in one fell swoop. Although, the result is messy...

$$ 2 = \dfrac{1 + \dfrac{\sqrt{3} }{\tan \theta} }{\sqrt{1+ \dfrac{3}{4 \sin^2 \theta} } } $$
Extreme algebra up ahead! Try to follow me. We algebraically simplify by cross-multiplying, then squaring both sides.

$$ 4 + \dfrac{3}{sin^2 \theta} = 1 + \dfrac{2\sqrt3}{\tan \theta} + \dfrac{3\cos^2 \theta} {\sin^2 \theta} $$
Combine like terms and divide both sides by three:

$$ 1 + \dfrac{1}{sin^2 \theta} = \dfrac{2}{\sqrt3 \tan \theta} + \dfrac{\cos^2 \theta} {\sin^2 \theta} $$
Now, there's a trick here. Combine both terms with $sin^2 \theta$ and you will see a trig identity.

$$ 1 = \dfrac{2}{\sqrt3 \tan \theta} + \dfrac{\cos^2 \theta - 1 } {\sin^2 \theta} $$
The latter term on the right side simplifies to $-1$ because of the Pythagorean Identitity. This simplifies the problem.

$$ 2 = \dfrac {2}{\sqrt 3 \tan \theta} $$ $$ \tan \theta = \dfrac{1}{\sqrt3} $$
Therefore, we can conclude that:

$$ \theta = \bbox[3px, border: 0.5px solid white]{ 30° }$$
Think back to what the problem originally asked: to show that a 2D elastic collision between two identical objects resulted in their final velocities being at right angles to each other. And we've just shown that, since the other angle is 60°!

There's a way to generally prove this, but the algebra for that is probably going to overload your brains after that one. So, we'll refrain from proving it here. You can give it a shot, though! Just generalize the problem to have $\theta_1$ and $\theta_2$ and try to algebraically manipulate the equations until you show they add to 90°, if you dare.

We can use the idea of vector components to split each momentum vector into its components. The total sum of final momenta in each direction must equal the initial momentum in that direction. It's much like one-dimensional collisions, but with an extra dimension or two thrown in that you need to worry about.

A word of caution. You cannot use the relative velocity formula I gave before; it only works for a one-dimensional elastic collision. The reason behind this has to do with center-of-mass velocity, which the formula depends on. In 1D, both the final velocities must lie on the same line as the direction of the center-of-mass velocity, but this constraint isn't true when we have two or more dimensions. The objects can move any which way they want, and are not constrained to a line.

With that said, I do want to emphasize that while conceptually two-dimensional and three-dimensional collisions are very simple, mathematically they can be an absolute nightmare. For an inelastic collision, things are simple as always, but the elastic collison requires you to solve a system of three equations, with trigonometry thrown in as well just for "fun".

If you want to glimpse into the maw of the beast, you can peek at our algebra-based level and look at the practice problem there.

One interesting result (that you don't need to derive because it's mathematically complex) is that if one object elastically hits an identical one, their final velocities will be at right angles to each other. A neat result that can be used to solve certain problems very quickly. Here's the scenario I'm talking about, drawn out:

Conclusion